Dungeon Generation Revisited

Keywords: relative neighborhood graph, room connection, room placement, connection graph, connection structure, dungeon generation, method, map, random, discard, maze, lead. Powered by TextRank.

Dungeon generation

There are a couple of different ways I've seen around the web for dungeon generation for rectangular rooms

Tunneler
Relative Neighborhood graphs
BSP

It's safe to say you can breakdown dungeon generation into 2 base components

Room placement
Room connection

Room placement

The placement can be done at a random fashion by generation of room at random x,y with random width and height. The coordinate selection can be normally distributed, the w/h generation can be normally distributed or have a gaussian distribution. It's likely that rooms generated this way will intersect. To deal with the you can either discard a room that overlaps with another room and continue generation until MAX_TRIES or the desired number of rooms has been reached. Another method is to space out rooms until non are overlapping and discard any rooms that have "fallen off" the edge of the map.

*method 1 - discard overlapping rooms*

for _ in 0...maxRooms {
    let w = Int.random(in: minRoomSize...maxRoomSize)
    let h = Int.random(in: minRoomSize...maxRoomSize)
    let x = Int.random(in: 0..<cols - w)
    let y = Int.random(in: 0..<rows - h)
    let newRoom = Room(id: roomId, xy: XY(x: x, y: y), wh: WH(w: w, h: h))
    roomId += 1
    let failed = rooms.contains { newRoom.intersects(other: $0) }
    if !failed {
        renderer.drawBox(x: x, y: y, w: w, h: h)
        rooms.append(newRoom)
    }
}

*method 2 - push out rooms until they don't intersect anymore*

var touching = true
while touching {
    touching = false
    for i in 0..<numRooms {
        for j in (i+1)..<numRooms {
            let a = cells[i]
            let b = cells[j]
            if a.intersects(other: b) {
                touching = true
                var dx = min(a.bottomRight.x - b.topLeft.x + padding, a.topLeft.x - b.bottomRight.x - padding)
                var dy = min(a.bottomRight.y - b.topLeft.y + padding, a.topLeft.y - b.bottomRight.y - padding)
                if abs(dx) < abs(dy) {
                    dy = 0
                } else {
                    dx = 0
                }
                let dxa = Int(-dx / 2)
                let dxb = dx + dxa
                let dya = Int(-dy / 2)
                let dyb = dy + dya
                a.shift(dv: XY(x: dxa, y: dya))
                b.shift(dv: XY(x: dxb, y: dyb))
            }
        }
    }
}

Room connection

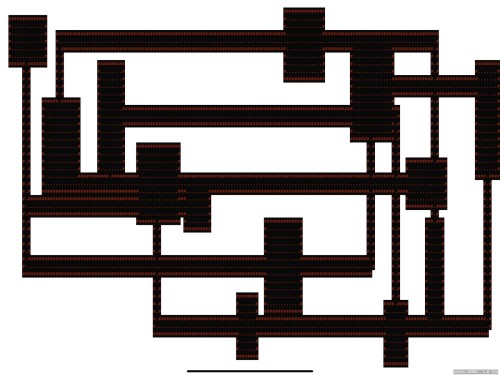
Connecting rooms can be done by connecting the current room with the one before it. You can have a X% chance of initiating the connection from the top of the room or the side of the room to add some flavor. This method guarantees that the dungeon is fully connected and usually as the number of rooms increase you get a cyclic connection structure which is more interesting than a non-cyclic structure. Using this method can lead to a direct connection from the start room to the end room. There are checks that could be implemented to mitigate this and the game mechanics may also give incentive to exploration to make this a non-issue. I call this the “n-1” connection/tunneler method.

if !failed {
    renderer.drawBox(x: x, y: y, w: w, h: h)
    let newX = newRoom.centerX
    let newY = newRoom.centerY
    if rooms.count != 0 {
        let prevX = rooms.last!.centerX
        let prevY = rooms.last!.centerY
        if Int.random(in: 0...10) < 5 {
            horTunnels.append((x0: prevX, x1: newX, y0: prevY))
            vertTunnels.append((y0: prevY, y1: newY, x0: newX))
        } else {
            vertTunnels.append((y0: prevY, y1: newY, x0: prevX))
            horTunnels.append((x0: prevX, x1: newX, y0: newY))
        }
    }
    rooms.append(newRoom)
}

The example code just stores the coordinates of the halls that are created and doesn't store the connection graph but that pretty trivial to implement but it's not needed as the level map provides this data after the tiles are laid on the map.

Another method of connecting the rooms is to use Relative Neighborhood Graphs. This is a subgraph of the Delauny Triangulation and tries to connect rooms that appear to be close and produce nice results. If this type of graph feels to strongly connected creating a MST for the rooms and then selectively adding X% percent of the RNG connections that may also yield good results.

Halls

The connecting halls them selves can either be straight, L shaped or meandering like a maze. Maze algorithms may lead to dead ends which may not be desirable but can easily be pruned (just remove any hall tile that surrounded by at least 3 empty tiles).

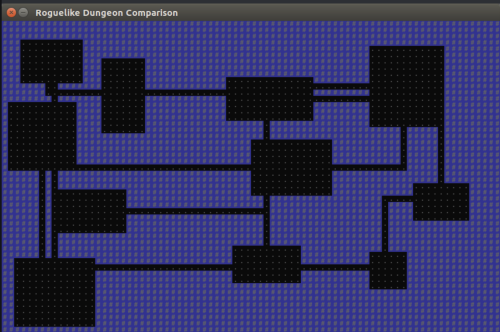
*a map generated by random intersecting prune placement and n-1 tunneling*

a.md.jpg

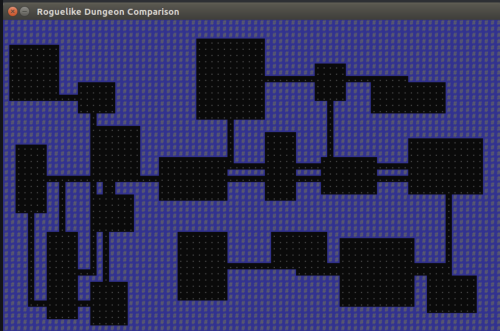
another map generated by the same algorithm as above (someone else wrote this, I saw their post on reddit in /r/roguelikedev but can't find it anymore so I can't properly credit them)

b.md.png

BSP made room placement with n-1 connection

c.md.png

Maze based tunnelling

d.md.png

Metadata

741 words

Dungeon Generation Revisited