Keywords: target cell, movement cost, neighbor cell, current cell, rasterization algorithm, path, ship, distance, lead, heuristic, check, select. Powered by TextRank.
Up until now there were any obstacles (excluding ship) so I really didn’t care for a proper path finding algorithm to select the cells that the ship would follow to reach it’s target. A simple rasterization of the cells were the way to calculate the path, but since I’ve added some asteroids it I also thought I’d spice up the path finding too.
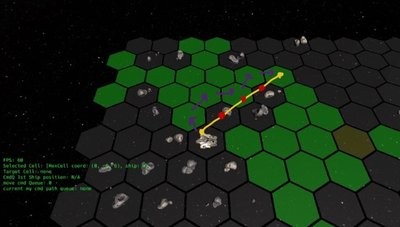
In this picture the rasterization algorithm would pick the yellow line and the cells with the red dots on them, which are actually obscured by asteroids. The correct path is the path with the purple arrows. How to you choose these? Well luckily there are a couple of ways. The brute force version would be to do a breadth first search to find the target cell which would lead to wasted movements for sure. The next best approach is the select the next cell in the BFS not at random or in order but based on a heuristic, a good guess to which cell would lead quicker to the target cell. The easiest heuristic that comes to mind is the hex distance calculated as Math.max( x2-x1, y2-y1, z2-z1). You also add the total cost of movement to this cell, something that you know for sure. Why do we add the cost of movement? Because we may need a rotation to get to that neighbor cell, which is also a movement cost. So from the starting cell, you look at all the neighbors and calculate the distance to the target cell + the cost of movement to that cell and choose the closest one. You add the current cell to the visited list. Why? because in the next step the current cell will show up as a neighbor, and we don’t want to check that cell again. Then you advanced to that cell and do the same until you have reached your target. Is it possible that the target cell is never found or a ship will be there to block us? No because the target cell validity check is done before hand (the green cells). This is a simplified version of the A-start algorithm. Here it is in action
video was lost (h4.gif)
Powered by TF-IDF/Cosine similarity
First published on 2017-12-19
Generated on May 5, 2024, 8:47 PM
Mobile optimized version. Desktop version.