Hexarategy: Hex grid neighbors

Keywords: neighbor cell, neighbor list, direction array, se neighbor, se relation, sw neighbor, opposite neighbor, opposite direction, original cell, position, row, grid, nw, index. Powered by TextRank.

In the graph based storage of hex grids an important function for the cells is for them to keep track of their neighbor cells.

One way you can build the neighbors list is as you are constructing the grid itself. This can be done on a direction basis. Each cell has the following the directions:

NW (northwest)
NE (northeast)
E (east)
SE (southeast)
SW (southwest)
W (west)

We will use an array of size 6 in each cell to store the neighbors. Each position in the array will correspond to a direction. It doesn’t really matter which index is which position as long as your are consistent about it. If you use an enumeration structure you will automatically assign integers for each direction, which you can then use as the indices for the neighbors array. Keep in mid that not every cell has exactly 6 surrounding cells. Depending on the position on the board some cells may have 3 or 5 but never more than 6. Here is an example to clarify things:

Let’s assume the following values for the 6 directions:

NW = 0, NE = 1, E = 2, SE = 3, SW = 4, W = 5

And the Cell object will have a structure similar to Cell[] neighbors = new Cell[6];

if the cell we are looking at has a neighbor on the NW side, then neighbors[] will point to the neighbor cell. Incidentally the neighboring cells neighbors array would have the original cell at the SE (3) position. So this relation holds:

For cells with 6 neighbors the original cell is refers to it’s neighbors in a direction and the neighbors refer to the original cell in the opposite direction.

How can we calculate the opposite direction? Quite easy: The position you want + 3 modulo 6. The module will make the directions wrap around after reaching the end of the direction array.

Ok so let’s start of with the easiest direction: the W – E connection.

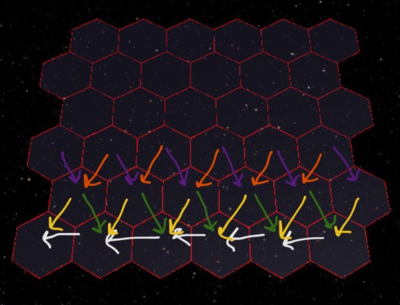
In this diagram the white arrows show the W-E relationship between cells. Remember that we are populating the neighbor list as we create the grid, so the neighboring cells must exist before we can add their pointers to the neighbor list. If we start from the bottom left corner, the first cell has no neighbors to the W, so we can skip that. On to the second cell to its right. This guy has a neighbor to the west so we can add this to the list, and the opposite neighbor relation also holds. We can do this for the rest of this row, and go on to the next row. On the next row, the same is true: skip the first add the rest. So the condition for creating the E/W relation can be written

function addCell(x,z,i) {
 
 if (x > 0)
 {
  cell.neighbors[W] = cells[i - 1];
  cells[i-1].neighbors[W + 3 % 6] = cell;
 }
 
}

The assumption here is that all the cells in the grid are stored in an array called cells. This is a 1 dimensional array. I felt that this may be a bit counter intuitive and deserved a remark. The function will be called for each X, Z coordinate with the position of the cell in the cells array.

For the SW and SE relations we need to distinguish between the cases of even and odd rows. Why? because the the first and last hex of the rows change which neighbors they have. The first element of the 2. row (index 1 so odd) has a SW and SE neighbor but the last hex is missing a SE neighbor. The first element of the 3rd row (index 2) is missing the SW neighbor. None of the cells on the first row have a SE or SW neighbor. So our conditions are:

if (z > 0 ) {
 if (z % 2 == 0) {
  ...
 } else {
  ...
 }
}

Let’s take a look at the even case, the purple and orange arrows:

The first cell doesn’t have a SW neighbor, so that’s will be a special case. The rest of the cells have both neighbors.

if (z % 2 ==0) {
 cell.neighbors[SE] = cells[i - width]
 //add the opposite too
 if (x > 0) {
  cell.neighbors[SW] = cells[i - width - 1] 
  //add the opposite too
 }
}
//The odd case (yellow and green arrows):
if (z % 2 == 0) {
...
} else {
 cell.neighbors[SW] = cells[i - width]
 //add the opposite
 if (x < width - 1) {
  cell.neighbors[SE] = cells[i-width+1]
  //add the opposite
 }
}

Metadata

764 words

Hexarategy: Hex grid neighbors

Metadata

Similar posts