Chess programming with bitboards part 4

Keywords: piece location, bit board, bit mask, bit set, attack vector, binary subtraction, rook, rank, borrow, shift, square. Powered by TextRank.

Now it's time to generate moves for sliding pieces: rooks, bishops and queens. I think this is one of the most ingenious ways of using bit manipulation. The idea is the following: Given a board with the square a sliding piece is on set how can we get all the attacks for that piece as a bitboard? Let's just assume we are computing this for a rook to make things easy. If the board was empty it would be pretty simple: Just come up with a mask that would set all the bits on the the rank for the piece and a mask that would set all the bits on the file. But the problem is that we can have a piece in our way that is blocking further movement for the piece. So consider the following board

If we were generating the horizontal moves for the rook and the rank was empty we would end up with

In this resulting board all the 1s indicate a square that is a valid move, so we cleared the origin square for the rook. But let's assume there is a friendly piece 3 squares to our left:

In this case our resulting bit board would be:

Since we cannot capture a friendly piece we would need to clear the position for that piece and any squares after that piece to the left. It's possible to come up with a bunch of rules like that implement them in an imperative manner but that would be a just a little bit more efficient than implementing a squares based algorithm and not worth all the weird bit masks. There is another method to compute the attack vector that exploits the properties of binary subtraction. To understand how this work let's first take a look at binary subtraction:

 100000110
-000000010
----------
 100000100

This is a straight forward case where there is no borrowing involved. But if you need to borrow then we borrow from the next bit that is a 1 to our left and that borrowing propagates through all the bits up to our location.

 100000110
-000001000
----------
(borrow from MSB)
 011110110
-000001000
----------
 011111110

How did I get a 1 after subtracting 1 from 0 on the 4 bit from the right? Well remember we borrowed to that 0 actual became a 10 in binary, and 10 - 1 = 1. The thing to notice here is how that borrow operation from the left bit sets all the bits upto the location we are subtracting from. This is exactly what we need to cast an attack ray. Using this in bitboards is called the o ^ (o - 2r) trick. It works like this: You get the occupied board (this is the o part) and then shift the position of the piece you need to calculate for to the left (this is the 2r part). Then you subtract the 2r from the o. This will propagate the borrowed bit all the way to the location of the piece we are calculating for. Let's apply this to the rook example above (I'm just showing rank 3)

01001000 3

So our piece is on bit 4 and the friendly piece is on bit 7. Let's write these out seperately:

01000000 3 (friendly)
00001000 3 (piece)

Why do we need to shift to the left? If we don't we'll just be clearing out our piece location and it would not get us anything.

01000000 3 (friendly)
00010000 3 (piece, shifted)

After we shift and subtract

01000000 3 (friendly)
00010000 3 (piece, shifted)
--------
00110000 (attack vector)

Our attack vector shows that we can attack 2 squares to the left. This trick only works towards the left of the bits as we need subtraction. To compute the attack in the other direction we just need to mirror the bitboard and run the same operation. Then we can combine the results from these, mask for the rank, file or diagonal we are interested in and return. This will automatically work for files, ranks and diagonals.

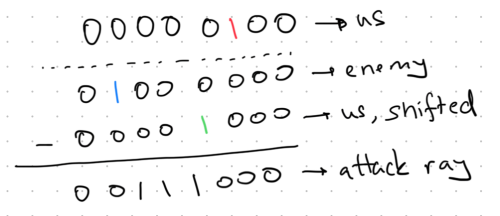
Here is another example:

Metadata

694 words

Chess programming with bitboards part 4

Metadata

Similar posts