Keywords: move object, piece move, san notation, origin square, pgn file, file information, passant square, pawn move, target square, board, check. Powered by TextRank.
Now that all the basic building blocks have been covered by the previous posts, it would be useful to take a step back and think about how all of this works together, especially regarding the edge cases of some of the special rules of chess.
Starting with a PGN parser is a good way to dive into this. Our goal is to import a chess game from a PGN file and be able to walk through the moves in the main line. But we also want to validate that all the moves in the PGN file are correct and valid. Parsing the PGN into a syntax tree is a problem of its own, which I wrote about before .
Assuming we have tokenized all the text and parsed it into some structure, we can traverse the nodes in this structure. When we encounter a move node, we can create a Move object from it and pass it to the board for execution. If it is a valid move, we'll append it to the list of moves in the main line. There are two points to consider here:
The first point is interesting because SAN notation does not mention coordinates but only the piece type (implicitly for pawns). To actually make a move, we need the source square of that piece. So, when creating a move from SAN notation, we need to pass in the current state of the board. It’s also helpful for the move object to contain additional information, such as the color of the piece and its type, as well as whether this move was a promotion or a capture. Here’s the information I tracked in my implementation:
init(
from: Square,
to: Square,
color: Color,
pieceType: PieceType,
capturedPieceType: PieceType? = nil,
promotion: PieceType? = nil
) {
...
}When decoding SAN notation, the idea is to handle castling separately, as the source, target, and piece are known. Then, check for special characters like "=", "x" that denote promotion and capture, and store these as we’ll pass them to the Move object initializer later. Next, check if it's a pawn move by looking at the first character—other piece moves always start with an uppercase letter. The remaining part contains the target square for the move. You also need to account for tricky cases like promotion captures (e.g., dxc8=Q , which means that the pawn on the D file captures something on c8 and promotes to a queen).
The final missing piece is the origin square. To find this, you need to get the bitboard for the piece type you’re checking and iterate through it to find possible movement squares. When iterating through all possible moves, if any of them match the square extracted from SAN, we then need to make sure it’s a legal move (e.g., not leaving the king in check). If the move is legal, we append it to a list of candidate origin squares.
Why a list? It’s possible for two pieces of the same type to move to the same target square (e.g., two rooks on A and H files moving to c1). In this case, SAN notation, like Rc1 , must be disambiguated. At the end of the loop, consider the following cases:
For case 0, either the PGN is invalid or there’s a bug in our code. In case 1, we can use the square. For case 2, we need to further process the SAN to disambiguate the piece’s origin square. The SAN notation will contain file or rank information after the piece name, which we can parse to filter our candidate origin squares. The SAN can also contain both rank and file information simultaneously, but I haven’t encountered that yet. With this, we have all the information required to create and validate a Move object from the SAN, which we can then send to the board for execution.
In the execution function, additional validation is necessary, such as:
Remember, we are receiving an arbitrary Move object that could have any origin and target squares, so we need to rigorously validate the move. Once validations pass, we force the move, even if it would leave the player in check, and then check if it does. If the move leaves the king in check, we undo it and return an error, as the move is illegal.
If the move is a castling move, we update castling rights. We also need to check if the move would allow an en passant capture next turn. En passant occurs when a pawn makes a double move and lands adjacent to an enemy pawn, which may capture to the square behind the pawn. If the double move results in a check or capturing en passant would leave the king exposed (e.g., the pawn is pinned), the en passant square cannot be set. Processing 100K games taught me all these en passant rules :)
Next, we update the move counters, and the execute function is almost complete.
In the force move function (called within execute), I maintain the threefold repetition counters. This is essentially a dictionary of the board's hash and an integer that tracks how many times the position has occurred. The board hash is a Zobrist rolling hash containing piece locations, castling rights, the en passant square, and which side is to move. You also need to push the current move to a stack so that it can be undone if necessary.
Adjust the bitboards for the piece that moved: remove the bit for the origin square and set the bit for the target square. If there’s a capture, also adjust the bitboard for the captured piece and clear its bit. For a promotion, adjust both the source piece and the new promoted piece’s bitboard. For castling, adjust castling rights, and if the move involves a king or rook, or a rook is captured, reset castling rights accordingly. Finally, set the side to move to the opponent’s color, and you’re done.
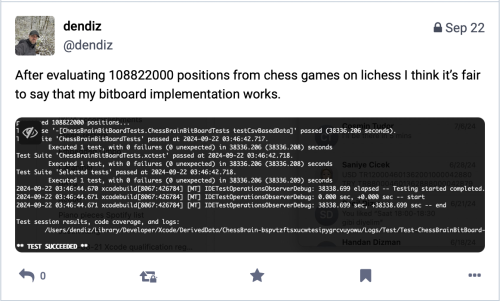
There are many edge cases and intricacies when implementing chess rules. A great way to test your implementation is to compare the board FENs with those generated by another parser. I downloaded a Lichess PGN database with millions of games and ran the first 100K through pgn-extract to add the FEN after each move as a comment. Then, I put together a small Python script to read the PGN file and output a CSV with the columns:
before_fen,san,after_fen
In my test cases, I would load the PGN, compare the board’s FEN to the CSV file, make the move, and compare the resulting FEN to the CSV. I processed around 108 million moves from these games as tests, encountering all sorts of edge cases.

1179 words
Powered by TF-IDF/Cosine similarity
First published on 2024-10-04
Generated on 11 Aug 2025 at 12:23 PM
Mobile optimized version. Desktop version.