
Keywords: map array, pgn file, pgn game, pgn method, chess move, chess game, chess board, piece move, move method, move list, heat map, chesspresso pgn, square, spark. Powered by TextRank.
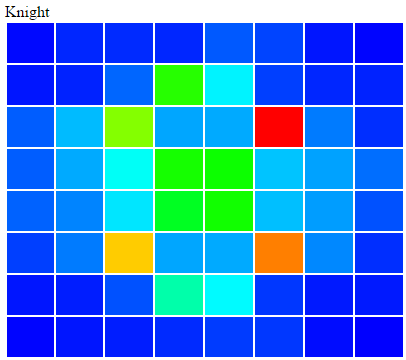
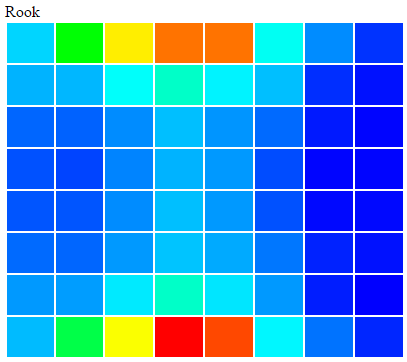
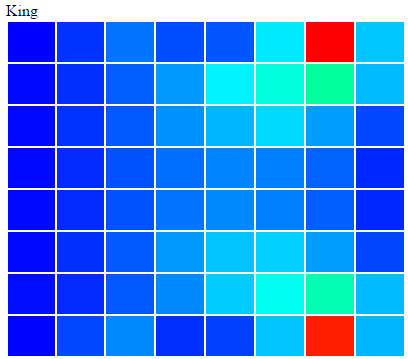
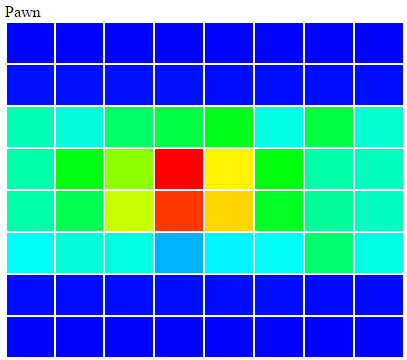
The apache spark framework is a great way of processing HUGE amounts of data in parallel. The learning curve is really flat, and you’ll get to crunching data in no time. I have already implemented a batch log processing / analytics application and a real-time streaming application at work for n11 and I thought that I do another fun project with spark. This time it’s generating a heat-map of a chess board by processing chess games. A heat map of a chess board is 8×8 table with each cell representing a square of the chess board with a color. Blue means there were not many moves to that square, and red means there were a lot. It’s an analogy to the warm-cold method of defining distance. We will do this for each piece there is in chess. The end results will look something like this

So, a method we could use and that I’ve tried was to generate a FEN representation of the board after each move, and feed this data to apache spark to extract how much each piece occupied each square. This did sound reasonable and it would have been very efficient because spark would not need any chess knowledge to compute the heat map. Just some string parsing would suffice. But it turns out that this method of processing overwhelms the heat map with the initial positions of the piece. Why? because the pieces rest on their initial squares for quite some time before they move. Let’s look at an example to make it clearer. The initial state of the board as a FEN string is:
rnbqkbnr/pppppppp/8/8/8/8/PPPPPPPP/RNBQKBNR
this would mean add 1 to the squares for each piece. E.g the rooks are on a1, a8, h1, h8. Add 1 to each square. After the first move, say 1. e4, the FEN is
rnbqkbnr/pppppppp/8/8/4P3/8/PPPP1PPP/RNBQKBNR
The pawn will register a hit for the e4 square, but so will all the other remaining pieces for their home squares! The will generate a heat map that says all the pieces like their home squares best which isn’t really helpful.
So we need another approach. The best way is to register a square that a piece has moved to. This requires parsing the moves in the PGN game and actually playing through the game. So we need a chess parsing library to use in our spark job. Fortunately I had a nifty little port of chess.js for java handy here that would allow me to play through the games and get back the squares the pieces moved to. But before we can dive into this, we need to clean the PGN files and make them suitable for processing by Spark. Data processing platforms like spark like to munch data that are in CSV format – a line of values separated by a comma. The values in our file will be the moves from each game, starting from the initial position. Here is an example of what I mean
d4,Nf6,c4,e6,Nf3,d5,Nc3,Be7,Bg5,h6,Bh4,O-O,e3,b6,Bd3,Bb7, O-O,Nbd7,Bg3,c5,cxd5,Nxd5,Nxd5,Bxd5,Rc1,Nf6,dxc5,Bxc5,a3,a5, Qe2,Nh5,Be5,Bxf3,gxf3,Qg5+,Bg3,g6,Rc4,Rfd8,Rd1,Rd5,Rg4,Nxg3, hxg3,Qf6,Rf4,Qg5,Rg4,Qf6,Rf4,Qg5,Rg4,Qf6 e4,c5,Nf3,d6,d4,cxd4,Nxd4,Nf6,Nc3,a6,g3,e6,Bg2,Be7,O-O,O-O,a4, Nc6,Be3,Rb8,f4,Qc7,Kh1,Bd7,Nb3,b6,g4,h6,Qe2,Nb4,Nd4,Rbc8, Rad1,Qc4,Qf3,e5,Nf5,Bxf5,exf5,exf4,Rd4,Qc7,Bxf4,Nxc2,Rd2,Nb4,h4, Nh7,g5,Qc4,f6,gxf6,gxf6,Bxf6,Ne4,Be5,Rxd6,Bg7,Bxh6,Bxh6,Rxh6,Rc6,Qg4+,Kh8,Rxh7+
So let’s dive into converting the PGN files.We will use the excellent chesspresso library to parse the PGN files because I haven’t yet integrated PGN methods into chesslib. the dependency for chesspresso can be added using
resolvers += "clojars.org" at "http://clojars.org/repo" libraryDependencies += "com._0xab" % "chesspresso" % "0.9.2"
Thanks to the guy who was kind enough to package and upload this to a repository. Meanwhile I’m not so nice and haven’t uploaded chesslib to a repository, but no problem we’ll just add it to the /lib directory and the sbt assembly plugin will pick it up from there. So let’s start by parsing the PGN files using chesspresso
def getGames(file: File) : Stream[Game] = {
val fis = new FileInputStream(file)
println("parsing file " + file)
val reader = new PGNReader(fis, "")
val games = di2(reader)
//println(file + "... found " + games.size + " games")
games
}this method expects the PGN file as a File object, and reads it using the chesspresso PGNReader.
def di2(reader:PGNReader): Stream[Game] = {
@tailrec
def di3(game:Game, reader:PGNReader, gameList : Stream[Game]): Stream[Game] = {
if (Option(game).isDefined) {
if (gameList.size % 5000 == 0) {
println("processing game " +gameList.size + " " + game)
}
//println("found game " + game + " list size " +gameList.size )
di3(try {reader.parseGame()} catch{ case e:Exception=>reader.parseGame()},reader, game #:: gameList)
} else {
gameList
}
}
di3(reader.parseGame(), reader, Stream.empty)
}this is the actual method that reads the games to a list. Chesspresso iterates over the games and streams the games from the file on demand (because PGN files may contain more than one game). Since we are consuming the whole stream this will not work if you try to process a PGN file with lots of games in it (around 1M suffers on my 8gb machine). If you need to split a PGN file to smaller files use pgn-extract.
def extractMoves(game:Game) : String = {
game.gotoStart()
try {
val mainLine = game.getMainLine.toSeq
val moves = mainLine.map(x=> {
game.getPosition.doMove(x)
x
}).toList.filter(_ != "")
moves.mkString(",")
} catch {
case e:Exception=>""
}
}This method will get the moves made in the game as a list and concatenate them using a comma to the CSV format that I showed you above. Chesspresso will throw an exception on an invalid move, and some PGN’s do contain invalid moves.
def main(args:Array[String]) = {
val hotFolder = "/data/pgn/archive/"
val outFolder = "/data/fen/"
val files: Seq[File] = new File(hotFolder).listFiles().toSeq.filter(_.getName.endsWith("pgn"))
files.foreach({file=>
val games = getGames(file)
val moves = games.map(extractMoves)
val target = new BufferedOutputStream( new FileOutputStream(new File(outFolder+file.getName + ".moves")) )
try moves.foreach({x=> target.write(x.getBytes); target.write("n".getBytes) }) finally target.close
})
}All that’s left is to execute the parsing methods and save the CSV move list to a file and we are ready to jump into spark to process this data. Thats what the main function above does.
So let’s define some spark configs like the CSV file location etc.
val logFile = "/data/fen/" // Should be some file on your system
val outputDir = "/tmp/"
val conf = new SparkConf().setAppName("Simple Application")
val sc = new SparkContext(conf)
val moveData = sc.textFile(logFile)we will also need a data structure to hold the results, how many times each piece moves to a square.
val map = Map(
"r" -> Array.fill(64)(0),
"n" -> Array.fill(64)(0),
"b" -> Array.fill(64)(0),
"k" -> Array.fill(64)(0),
"q" -> Array.fill(64)(0),
"p" -> Array.fill(64)(0)
)this map can be though of like this: the keys represent each piece (the colors are irrelevant) and the values are an array of size 64 – one slot for each square on the chess board. When a piece moves to a square we will increment the count in the array.
val mmap = Map(
"a8"->0, "b8"->1, "c8"->2, "d8"->3, "e8"->4, "f8"->5, "g8"->6, "h8"->7,
"a7"->8, "b7"->9, "c7"->10,"d7"->11,"e7"->12,"f7"->13,"g7"->14,"h7"->15,
"a6"->16,"b6"->17,"c6"->18,"d6"->19,"e6"->20,"f6"->21,"g6"->22,"h6"->23,
"a5"->24,"b5"->25,"c5"->26,"d5"->27,"e5"->28,"f5"->29,"g5"->30,"h5"->31,
"a4"->32,"b4"->33,"c4"->34,"d4"->35,"e4"->36,"f4"->37,"g4"->38,"h4"->39,
"a3"->40,"b3"->41,"c3"->42,"d3"->43,"e3"->44,"f3"->45,"g3"->46,"h3"->47,
"a2"->48,"b2"->49,"c2"->50,"d2"->51,"e2"->52,"f2"->53,"g2"->54,"h2"->55,
"a1"->56,"b1"->57,"c1"->58,"d1"->59,"e1"->60,"f1"->61,"g1"->62,"h1"->63
)this second mmap array is a mapping from the string (SAN) notation of a square to it’s place the array that I mentioned above. We will need this because chesslib’s internal representation of a chess board as an array is different than what we will be using. Now let’s get to crunching those chess moves:
val key = moveData.flatMap(line=> {
// the maps above are here - omitted for readability
val cl = new ChessLib()
cl.reset()
val moves = line.split(",")
moves.foreach(move=> {
try {
val resultMove = Option(cl.move(move))
if (resultMove.nonEmpty) {
val piece = resultMove.get.piece
val to = resultMove.get.strTo
map(piece)(mmap(to)) += 1
}
} catch { case _ => }
})
map.toSeq
}).groupByKey()
val map1: RDD[(String, List[Array[Int]])] = key.map(x=> (x._1, x._2.toList))we start by mapping each line in our input. We initialise a chesslib instance that we will use to process the moves and reset to the starting position of a game. Next we split the CSV into a list of moves and for each move we make chesslib play that move. The result of the move method contains the piece and the square that the move was made to. We take that square and increment the count in the array contained in the map. We will need some grouping to we convert the map into a sequence. So before the sequence the result will be something like
Map("r"-> Array(10, 15, 20, 2, ...) //64 of these numbers
Map("r"-> Array(11, 25, 10, 1, ...) //64 of these numbersafter the conversion to a sequence we will have
("r", Array(10, 15, 20, 2, ...)), ("r", Array(11, 25, 10, 1, ...)), ...Why do we need this? because we will merge these maps to sum all the values in the arrays for each piece. The above example states that the rook was on a1 10 times in game 1 and 11 times in game 2. So the heat map will contains 21 for the rook on a1. When we group this sequence by key using the spark provided groupByKey method we will have the following result
("r" -> List(Array(10, 15, 20, 2, ...), Array(11, 25, 10, 1, ...) )we need to add the corresponding indexes in each array to obtain our result. We will use a helper function for this called combineLists
def combineLists[A](ss:List[Array[A]]) =
(ss.head.map(List(_)) /: ss.tail)(_.zip(_).map(p=>p._2 :: p._1))this methods takes a list of arrays, and returns a list of zipped lists. To for the input
List(1,2,3), List(5,6,7), List(7,8,9)
we will get the output
Next we need to sum the values in the combined lists for a our final result
val map2: RDD[(String, List[Int])] = values.map(x=> (x._1, x._2.map(_.sum).toList))
this will give us the total numbers of moves to each square for each piece. Just what we needed for the heat map! But we still need to do one more thing before we can start the rendering of the map and that is to normalise the values in the array to values between 0 and 1. We can do that using the feature normalisation formula
$$ X' = frac{X - X_min}{X_max - X_min} $$
the code is like this
val map3: RDD String, List[Double])] = map2.map(x=> (x. 1, x. 2.map( y=> (y - x. 2.min) / (x. 2.max.toDouble - x. 2.min) )))
now let’s create our map files as HTML pages with a table containing the heat map
map3.collect().foreach(rdd=> {
val tpl
html(rdd.
1, rdd._2.mkString(","))
new PrintWriter(outputDir + rdd._1 + ".html") { write(tpl); close}
})the html() function used here is a string template that uses the values between 0 and 1 to create a HLS color for a 5 color heat map. check out the code in the repo – it’s too verbose to include it in this post.
That’s about it on how to generate a chess board heat map. Here are the results for 1.5M games analyzed:

[image](https://img.dendiz.xyz/image/5Qeb)
[image](https://img.dendiz.xyz/image/5Cb7)
[image](https://img.dendiz.xyz/image/5dpt)
[image](https://img.dendiz.xyz/image/5z2E)
[image](https://img.dendiz.xyz/image/9tDd)
1730 words
Powered by TF-IDF/Cosine similarity
First published on 2015-09-20
Generated on 11 Aug 2025 at 12:22 PM
Mobile optimized version. Desktop version.